Wie das Ganze so der Teil

Es gibt seit den Pythagoräern die Überzeugung dass die Welt durch mathematische Prinzipien gestaltet ist und dass dies einheitlich der Fall ist, d.h. im ganzen Universum gelten die gleichen Prinzipien. Dieses Universalitätsprinzip besagt, dass die fundamentalen Gesetze der Physik und die grundlegenden Naturkonstanten überall im Universum gleich sind, unabhängig von Ort, Zeit oder den spezifischen Bedingungen eines Ortes. Das erinnert an die aus der Spätantike überlieferte hermetische Regel "wie oben so unten"; sie drückt die Vorstellung aus, dass es eine Wiederholung oder Ähnlichkeit zwischen den verschiedenen Ebenen des Kosmos gibt. Es besagt, dass das, was im Mikrokosmos geschieht, in irgendeiner Weise das widerspiegelt, was im Makrokosmos geschieht, und umgekehrt. Mathematisch passt zur Beschreibung dieses Sachverhalts das Konzept der Selbstähnlichkeit; es beschreibt die Eigenschaft von Gegenständen oder geometrischen Objekten, die in verschiedenen Größenmaßstäben stets wiederkehrende Strukturen aufweisen. So ist ein Baum ein Gebilde von Ästen, die ihrerseits einem Baum ähneln. Jeder Ast ist ein Gebilde von Zweigen, die ihrerseits einem Ast und wiederum einem Baum ähneln. Entsprechendes gilt für den Aufbau des Universums: Die Sterne einer Galaxis umkreisen das galaktische Zentrum. Jede Galaxis besteht aus vielen Sonnensystemen, in denen die Planeten eine Sonne umkreisen, die meisten Planeten wiederum werden ihrerseits von Monden umkreist.

Die Fibonacci-Folge

Es gibt eine mathematische Struktur, die in sich selbst immer wieder die gleiche Struktur enthält, die Fibonacci-Folge (nach Leonardo da Pisa, genannt Fibonacci, 1170- 1240). Sie beginnt mit 0. Addiert man 1, (0+1) so erhält man 1 als nächstes Folgenglied: 0, 1, 1. Addiert man die zwei letzten Zahlen so ergibt sich 1+1=2, also: 0, 1, 1, 2. Die Summe der jetzt zwei letzten Zahlen ergibt 3: 0, 1, 1, 2, 3 ... Bildet man die Differenz aller Folgenglieder (jede Zahl minus Vorgängerzahl), so erhält man wieder die gleiche Folge, deren Differenzen wiederum die gleiche Folge ergeben ... bis ins Unendliche.

Füllt man die Ebene beginnend mit 1, 1 mit Quadraten deren Seitenlängen den Gliedern der Fibonacci-Folge entsprechen indem man diese linksumlaufend aneinanderlegt so bilden die um die Quadrate gezeichneten Viertelkreise annähernd eine Spirale (siehe nebenstehendes Video).

In der kontinuierlichen Form wäre dies eine logarithmische Spirale (in der Abb. rot). Sie windet sich unendlich oft um ihren Mittelpunkt ohne diesen zu erreichen. Alle Geraden durch den Mittelpunkt schneiden die Spirallinie unter dem gleichen Winkel. Ihr Radius nimmt mit jeder Umdrehung um den gleichen Betrag zu. Sie ist selbstähnlich - durch Drehung und zentrische Streckung lässt sie sich auf sich selbst abbilden.

Fibonacci-Folge und Goldener Schnitt

Wenn man die Quotienten der Folgeglieder (1:1=1 | 2:1=2 | 3:2=1,5 | 5:3=1,666...) bildet, so entsteht eine neue Folge von rationalen Zahlen, die sich im Unendlichen der Zahl Φ [fi:] des Goldenen Schnittes annähern. 

Der Goldene Schnitt ist die Teilung einer Strecke in 2 Abschnitte derart, dass der größere Abschnitt (Major) zum kleineren Abschnitt (Minor) das gleiche Verhältnis bildet wie die Summe der beiden Abschnitte zum größeren. Man benennt dies auch als stetige Teilung. Die Konstruktion des Goldenen Schnittes geht hier vom größeren Abschnitt aus, aus dem ein Quadrat gebildet wird. Dessen Seite wird gemäß der nebenstehend abgebildeten Konstruktion um den kleineren Abschnitt ergänzt. Insgesamt entsteht das sogenannte Goldene Rechteck. 

Der goldene Schnitt und Selbstähnlichkeit

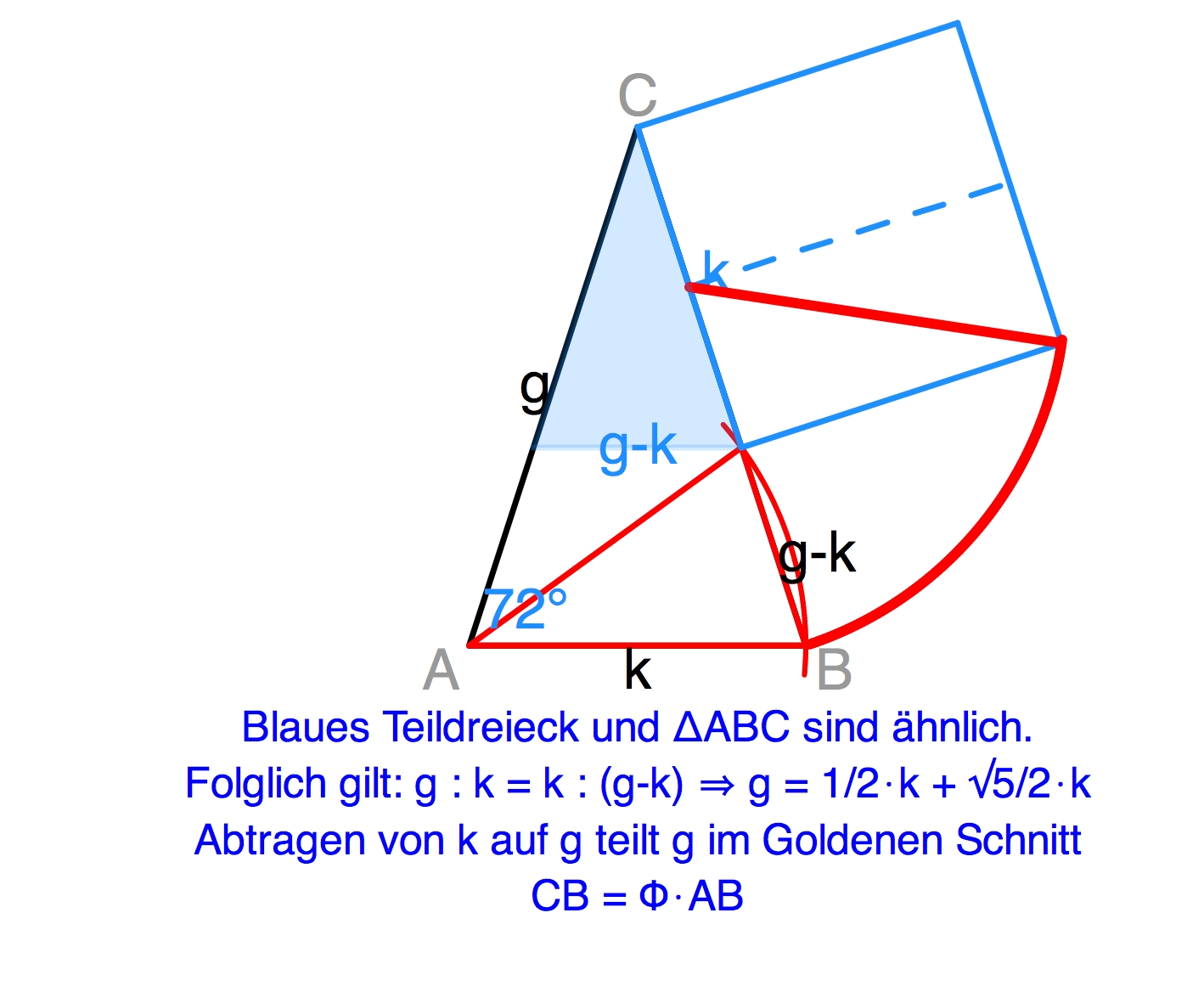
Das Goldene Dreieck ist ein gleichschenkliges Dreieck mit einem Basiswinkel von 72° (wie es zum Beispiel im Pentagramm ⛤ vorkommt). Durch Einzeichnen einer Winkelhalbierenden zum Basiswinkel entsteht ein Teildreieck, das an der Spitze den halben Winkel von 72° nämlich 36° aufweist. Es ist wieder gleichschenklig und damit im streng mathematischen Sinne ähnlich (WWS) zum ganzen Dreieck. Derselbe Vorgang lässt sich mit dem Teildreieck wiederholen - es entsteht also ein Teildreieck dritter Ordnung das wiederum zu seinen beiden Vorgängern ähnlich ist - und lässt sich unendlich oft fortsetzen.  Damit ist es möglich, die gesamte Figur auf einen Teil ihrer selbst abzubilden - es besteht also Selbstähnlichkeit. 

Man beachte dass der Begriff "Selbstähnlichkeit" hier im mathematisch strengen Sinne verwendet ist: Er setzt die Verkettung von Abbildungen wie Parallelverschiebung, Spiegelung, Zentrische Streckung in unendlicher Abfolge voraus. "Selbstähnlichkeit" als Formprinzip in der Natur wird ohne diese Strenge verwendet, da ja allein schon die Forderung nach Unendlichkeit für natürliche Objekte auszuschließen ist.

Verkettete stetige Teilung

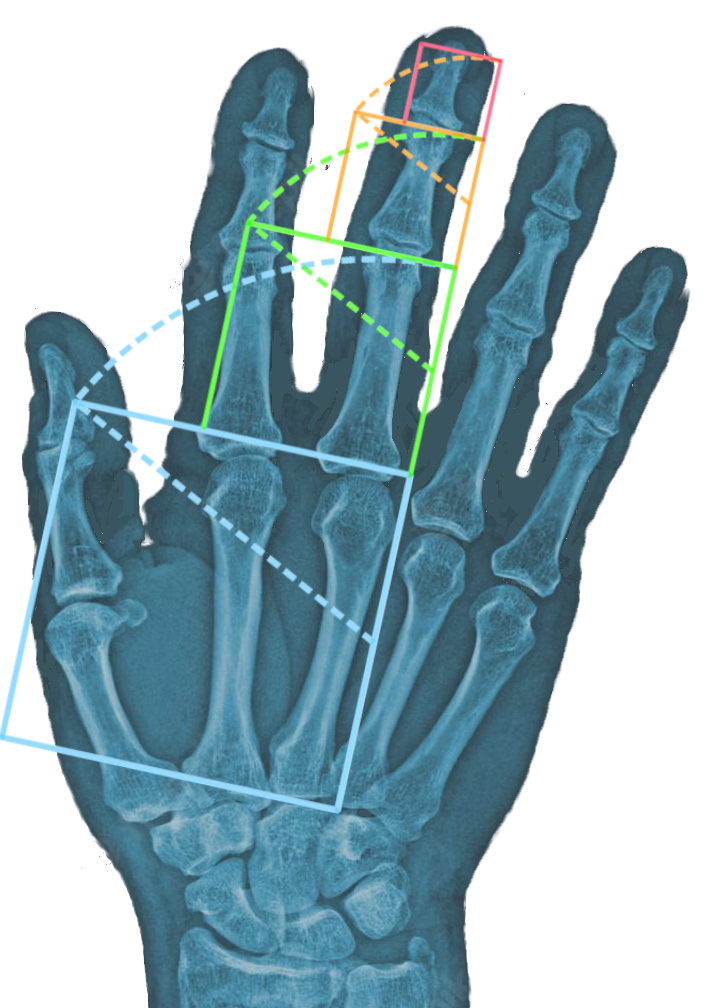
Wendet man den Goldenen Schnitt mehrfach an, konstruiert man also zum Major einer Teilung den Minor, und teilt diesen erneut, so entstehen Major und Minor zweiter Ordnung usw. - stetig kleiner werdend.  Z.B. entsprechen die Längen der Fingerknochen der menschlichen Hand einer solchen Verkettung von stetigen Teilungen. Hätten die Fingerknochen alle die gleiche Länge, so wäre der Haltegriff der gekrümmten Hand nicht möglich. Die Natur hat hier also eine durchaus zweckmäßige Konstruktion gefunden. 

Ähnliches gilt für die ringförmigen Muskelschichten des Elefantenrüssels, die sich zur Spitze hin stetig verjüngen. Auch die Verästelungen vieler Bäume folgen einer entsprechenden Regel: Die Astlänge nimmt nach jeder Verzweigung stetig ab. Die Länge des abzweigenden Astes ist im Durchschnitt der Minor der Länge des Stammastes (als Major).

Der Goldene Winkel

Eine Teilung des Vollwinkels von 360° durch die Zahl des Goldenen Schnitts Φ lässt zwei Winkel entstehen: 225,49...° und 137,5...°. Letzteren bezeichnet man als Goldenen Winkel. Er spielt in der Natur eine große Rolle, vor allem in der oft leicht erkennbaren regelhaften geometrischen Anordnung von Blättern, Knospen, Stängeln oder Fruchtansätzen und Samen von Pflanzen (man bezeichnet dies als Phyllotaxis - von "phyllon" für Blatt und "taxis" für Anordnung im Altgriechischen). Das Video zeigt die Entstehung dieses Musters aus einer fortgesetzten Drehung um den Goldenen Winkel 137,5...° bei gleichzeitiger Vergrößerung des Abstands vom Zentrum der Drehung. Bei den Blättern einer Pflanze garantiert diese Anordnung den optimalen Empfang von Sonnenlicht für jedes einzelne Blatt, bzw. minimale Beschattung durch andere Blätter. In gerechneten Simulationen zeigt sich, dass dieser Winkel in der Natur ziemlich genau eingehalten wird. Schon bei Abweichungen um 1° ist das Muster erheblich gestört.

Während alle Blätter, Knospen, Samen auf einer mehrfach die Mitte umkreisenden Spirale angeordnet sind, sind auch Scheinspiralen sichtbar, die schneller nach außen streben und nicht die Mitte umrunden. Davon gibt es rechtsorientierte und linksorientierte. Zählt man sie, so erhält man immer zwei unterschiedliche Zahlen: Aber es sind immer aufeinanderfolgende Zahlen aus der Fibonacci-Folge.

Bei Doldengewächsen (wie z.B. der Wilden Möhre) finden wir selbstähnliche Strukturen als Spiralen in Spiralen: Aus dem Stängel wachsen aus einer Knospe Stängel 2. Ordnung, die ihrerseits wieder in Stängeln 3. Ordnung ausknospen. Wir sehen Inseln mit der typischen spiraligen Struktur zu einer großen Spiralstruktur geordnet.